無線技術の初学者向けの論理回路の要点

細田 隆之


本稿では、論理回路に使用する図記号に、MIL-STD-806B が規定していた、いわゆる MIL 記号とその派生記号を用いています。 簡素な論理には MIL 記号での記述の方がひと目でわかりやすいからです。 図のためのグラフィカルなシンボル(Graphical symbols for diagrams)の規格 IEC 117-15 1972 (現在の IEC 60617) に於いても その使用は禁止されていません。
数学的にはともかく、IECの論理記号は 外形がみな四角であるためひと目では極めて判別しにくく、 論理変換や論理圧縮において利用しにくいものであったため、 論理回路設計者にあまり受け入れられませんでした。 禁止すると過去の回路図やドキュメントが読めなくなってしまうというのも理由の一つでした。
IECの論理記号があまり受け入れられなかったもう一つの理由は、 IECによる規定がされて程なく、1978 年の PAL (Programmable Array Logic) の登場により 論理回路の設計は HDL (Hardware Description Language) での記述に速やかに移行したためです。 複雑な論理回路を論理記号を用いた回路図で記述するのは現実的ではなく、 またコンピュータによる論理圧縮などの処理にも適していないからです。 1980年には PALASM, 1983年には CUPL, 1984年には Espresso algorithm を搭載した ABEL が使われるようになっていました。
1990年代以降、回路図においても論理回路の図記号の利用は、 部品間をつなぐいわゆるグルー・ロジック (glue logic) にとどまるようになったため、ひと目でわかる MIL記号は今でもポピュラーです。 グルーロジックとして多用される数個のゲートが入ったような IC のデータシートでは 2021年の現在でも MIL記号が多用されています。
論理回路において、いわゆる MIL記号では次の4つのシンボルを用います。
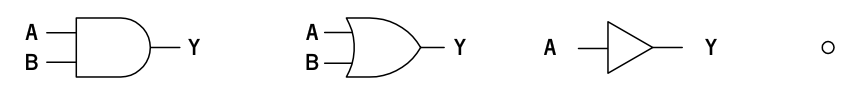
これは、左から AND (論理積)、OR (論理和)、BUF (緩衝増幅器)、NEG(logic negation, 負論理表示子) となっています。
AND では入力の全てが真(True)のときに出力が真となります。
OR では入力の何れかが真(True)のときに出力が真となります。
BUF では入力と出力の論理値は同じとなります。
NEG は論理演算において NOT と呼ばれます。
正論理であれば NEG (○印) をつけず、負論理であれば NEG (○印) をつけます。
真(True) を 1 で表し、偽(False)を 0 で表す時、正論理と呼びます。
真(True) を 0 で表し、偽(False)を 1 で表す時、負論理と呼びます。
BUF の入力または出力に NEG が1つ付いたものは慣例的に INV (インバータ)呼ばれます。
INV では入力と出力の論理値は反転します。
AND 回路の出力が負論理になっているものを慣例的に NAND と呼びます。
OR 回路の出力が負論理になっているものを慣例的に NOR と呼びます。
実際のロジック回路では、電圧(や電流)によって論理値を表します。
ある閾値より高い信号を H 、ある閾値より低い信号を L で表し、それぞれに 論理値を割り当てて使用します。
例) 実際の NAND ロジック IC (Integrated Circuit) MC74VHC1G00 の例
⚠️実際のロジック IC には電源の供給はもちろん、電源ピンの近傍にデカップリングキャパシタが必要です。
MC74VHC1G00 では、入力 A, B が全て H になった場合に、L が出力 Y に出力されます。
MC74VHC1G00 を 3.0 V の電源電圧で使用するときの入力電圧は、2.1 V 以上が H、0.9 V 以下が L となります。
同様に出力電圧は電源電圧が 3.0V , 負荷電流が 4 mA 以内で、H のとき 2.34 V 以上、L のとき 0.52 V となります。
ゲートに同じ信号が入っている N-MOS と P-MOS は N-MOS がオンのとき P-MOS がオフになります。
これこそが、Complementary MOS と言われる所以でもあり、低消費電力の理由でもあります。
電流が流れる状態を真とした場合、直列のスイッチは論理積に、並列のスイッチは論理和になります。
CMOS ロジック・ゲートは、電圧制御スイッチで構成されていると考えられます。
NAND ゲートのシミュレーション回路例
上記 NAND ゲートの動作波形例 (3V/div, 25ns/div)
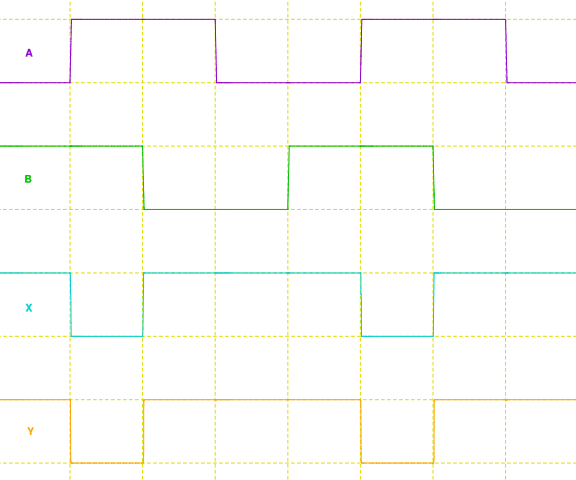
電圧が高い方を真とした場合には、入力が正論理で出力が負論理の AND と考えられます。
電圧が低い方を真とした場合には、入力が負論理で出力が正論理の OR と考えられます。
HDL の論理演算の表記は様々です。CUPL や ABEL 等の古典的 HDL を起源とする AHDL や、 C 言語風味な Verilog HDL、あるいは米国国防省の Ada の影響を受けた VHDL のようなものもあります。
NOT, AND, OR に加えた XOR (後述) は排他的論理和 (Exclusive-OR) を表します。EXOR と表す場合もあります。
AHDL では論理演算に次のような記号が用いられています。
記号 論理 ! NOT & AND # OR $ XOR
Verilog HDL では次のような記号が用いられています。
記号 論理 ~ NOT & AND | OR ^ XOR
VHDL では次のような記号が用いられています。
識別子と演算子が区別しにくいので個人的にはこんなの使いたく有りません。
記号 論理 NOT NOT AND AND OR OR XOR XOR
他にも、次のようなものがありましたが廃れました。
記号 論理 / NOT * AND + OR :+: XOR
例えば、入力が A, B 出力が Y の NAND 回路を HDL 記述すると
Y = !(A & B)
入出力とも負論理の AND は正論理の OR である。
いわゆる NAND 回路は負論理入力、正論理出力の OR であるともいえます。
一般に、入出力の論理を反転すれば、AND は OR に OR は AND になります。
!(A & B) = (!A # !B)
!(A # B) = (!A & !B)
!((A & B) # (C & D)) = (!A # !B) & (!C # !D)
- 定数との演算
(A & 1) = A
(A & 0) = 0
(A # 0) = A
(A # 1) = 1
(A $ 0) = A
(A $ 1) = !A — XOR は片方が1の時、入力を反転して出力するとも考えられます
- 自身との演算
(A & A) = A
(A # A) = A
(A $ A) = 0 — XOR は両方の信号が一致した場合に0を出力するとも考えられます
(A & !A) = 0 — 論理合成で使うことがある
- 吸収則 — 論理圧縮の時に良く使います
(A & B) # A = A
- 分配則 — 積和形式に直す時に良く使います
(A # B) & C = (A & C) # (B & C)
- 冗長項の追加 ― 出力のハザードの軽減や論理圧縮の途中で使うことがあります
(A & B) # (C & !B) = (A & B) # (C & !B) # (A & C)
- XOR の積和形式表現 ― PLDなどで XOR を合成するのに良く使います
(A $ B) = (( A & !B) #(!A & B)) (A $ B $ C) = (( A & B & C) #( A & !B & !C) #(!A & B & !C) #(!A & !B & C))
全ての論理式は、AND-OR の積和形式表現できます。入出力の論理の変更には INV を付加します。
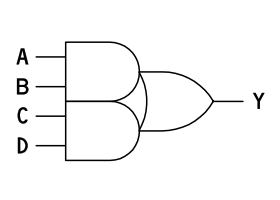
Y = ((A & B) #(C & D))のように AND による積を OR で足した形式を積和形式と呼びます。
このような形式で OR の数を最小にすることを(通常は)論理圧縮と呼びます。
ところで、B = !C とし、元の D を B に改めると、
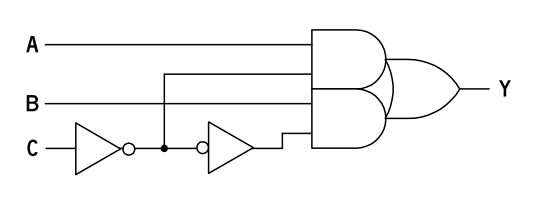
Y = ((A & !C) #(B & C))となり、C によって A, B の何れかを選択出力するセレクタと呼ばる論理回路になります。
ロジック IC や PLD (プログラマブル・ロジック・デバイス) や ROM (リード・オンリー・メモリー)も積和を元に構成されています。
先程のド・モルガンの法則を思い出して見ましょう。 2段重ねの NANDは 負論理出力の AND を負論理入力の OR で受けると捉えられますので、
 Y = !(!(A & B) & !(C & D)) = ( (A & B) # (C & D))NAND-NAND で 積和を構成することができます。
Y = !(!(A & B) & !(C & D)) = ( (A & B) # (C & D))NAND-NAND で 積和を構成することができます。
TTL では積和のために AND-OR-INV ゲートが使われていましたが、CMOS 論理 IC の中や、大規模プログラマブル論理デバイスでは、 NAND-NAND ゲートによって構成される AND-OR を利用して大規模な論理を合成することが行われています。
NAND が基本素子と言われるのは、NAND があればそれを組み合わせて全ての論理演算を行うことができるからですが、 実際の論理素子では多少ニュアンスが異なります。
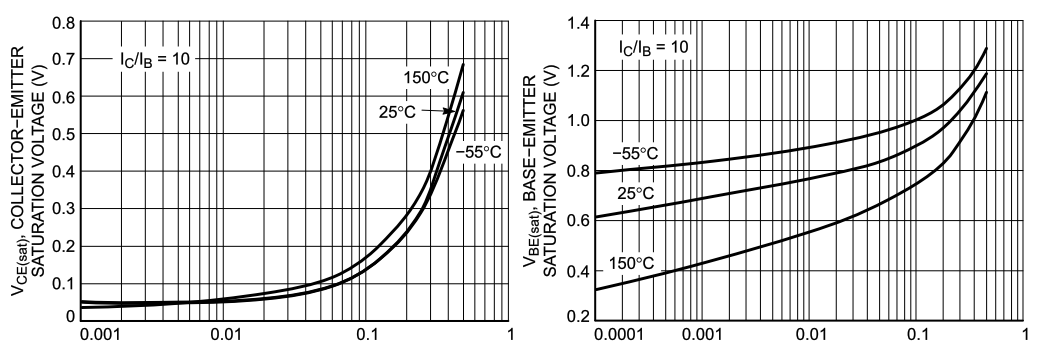
その昔、初期の半導体の論理素子は DTL (ダイオード・トランジスタ・ロジック) と呼ばれ、 ダイオードと NPN トランジスタで作られていました。 ダイオードを正論理の AND を構成するのに使用し、 NPN トランジスタのエミッタ電流を足して OR を構成し、 NPN トランジスタを反転増幅に使用するというのが基本構成でした。 この構成の基本論理素子を AND-OR-INVERT ゲート、略して AOI ゲートと呼びます。 AOI ゲートがあればすべての論理演算が可能です。 下図では、D1, D2 と D3, D4 でそれぞれ AND を構成し Q1, Q2 で OR を構成し Q3 で反転増幅して出力しています。 ここで、D3, D4, R3 と Q2 を端折れば NAND ゲートになりますし、D2, D4 を端折れば NOR ゲートになります。
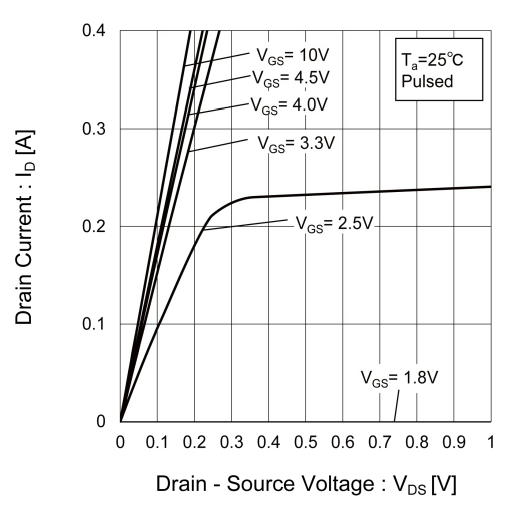
≡DTL や入力の AND 用のダイオードをマルチエミッタ・トランジスタに置き換えた TTL (トランジタ・トランジスタ・ロジック) あるいはトランジスタを非飽和で動作させる ECL (エミッタ・カップルド・ロジック)も21世紀には前世紀の遺物となり、 論理素子は高速な Low Voltage CMOS ロジックが全盛です。 CMOS は N-チャネル の MOS-FET の方がオン抵抗などの性能が良いので、N-MOS の方を重ね、 P-MOS の方を並列にして基本論理素子として NAND ゲートを構成します。 CMOS 1段での増幅度は小さいため、通常入力や出力に3段程度の INV が反転増幅器として入れられます。
≡
XOR は反転と積和を伴い、AND, OR, INV だけで表現すると煩雑になるため、専用のシンボルが使われています。
Y = A $ B = (( A & !B ) #( !A & B ))
この構成は、B が 1 のとき !A を、B が 0 のときに A を選ぶセレクタであると解釈することもできます。
CMOS XOR IC (e.g. CD4030) の中では使用トランジスタ数が少なくて済む次のような NOR + AOI 構成が用いられていました。
XOR は NAND だけを使って構成することもできます。
上記4つの NAND での XOR の構成例の論理式は、次のように変換できて論理合成の良い題材になっています。
Y = A $ B = ((A & (!A # !B)) #(B & (!A # !B))) = (( A & !A) #( A & !B) #( B & !A) #( B & !B)) = (( A & !B ) #( !A & B ))この4つの NAND を NOR に置き換えるとどうなるでしょう。
Y = !((!!(A # B) & !A) #(!!(A # B) & !B)) = !((A & !A) #(B & !A) #(A & !B) #(B & !B)) = (!A & !B) #( A & B)これは XOR の出力を反転したものとなっていて XNOR と呼ばれることがあります。 A と B が一致したときに Y が 1 となります。
- XOR は半加算器の下の桁です。
半加算器
一桁の値同士を足し算してみると、下の桁は入力の XOR、桁上がりは入力の AND となるのがわかります。
これを2つ組み合わせるとキャリー入力を備えた全加算器ができます。これは数値演算の基本となります。全加算器
CO = (( !A & B & CI ) #( A & !B & CI ) #( A & B & !CI ) #( A & B & CI )); S = (( A & B & CI ) #( A & !B & !CI ) #( !A & B & !CI ) #( !A & !B & CI ));上記、S の論理式は3入力 XOR としてよく利用されます。3入力 XOR のロジックICもあります。(e.g. 74LVC1G386)XORは、一桁の2の剰余系の加算器でもあります。 ある値同士を足して2で割った余りと考えることもできます。
実例:
これはパリティーチェックや CRC などの謝り検出や、誤り訂正など符号理論の応用の基本となります。(5, 2) ハミング符号の CoDec
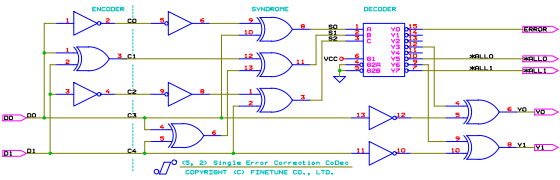
XOR回路は、ある信号の極性を別の信号で反転する回路と考えることができます。
実例:
これは変調器などの基本となります。QPSK 変調器 (部分)
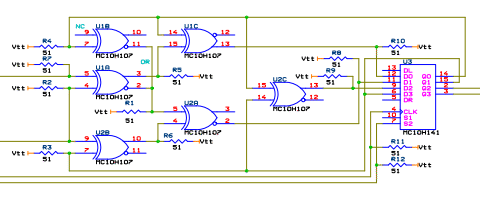
XOR は時間領域で見て、掛け算器とも呼ばれます。
実例 :
周波数領域でみるとこれは、周波数ミキサーとして働きます。
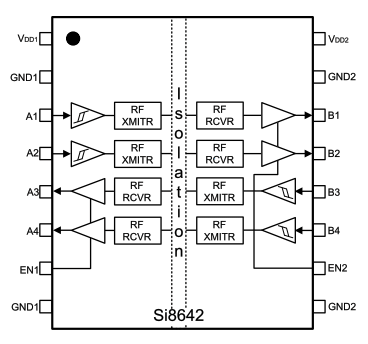
ダブルバランスドミキサーの動作は大雑把に言えば、XOR と同じです。下図のギルバート・セルのミキサーは 1, 4 ピンの差動入力で Q5, Q6 のコレクタ電流を作り、7,8 ピンの差動入力で Q1, Q2, Q3, Q4 でその出力先を切り替えています。 これは差動信号の電圧入力・電流出力の XOR と考えられます。
Renesas HFA3101
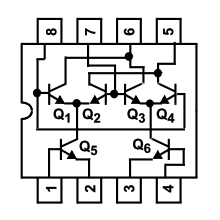
- XOR は位相比較器とも呼ばれます。
出力の区間積分あるいは平均値は、2つの入力信号の位相差に比例します。
XOR は無線回路技術者にとって重要な、 PLL を構成する位相比較器の基本となります。 実例 :Onsemi (Motorola), MC74HC4046B
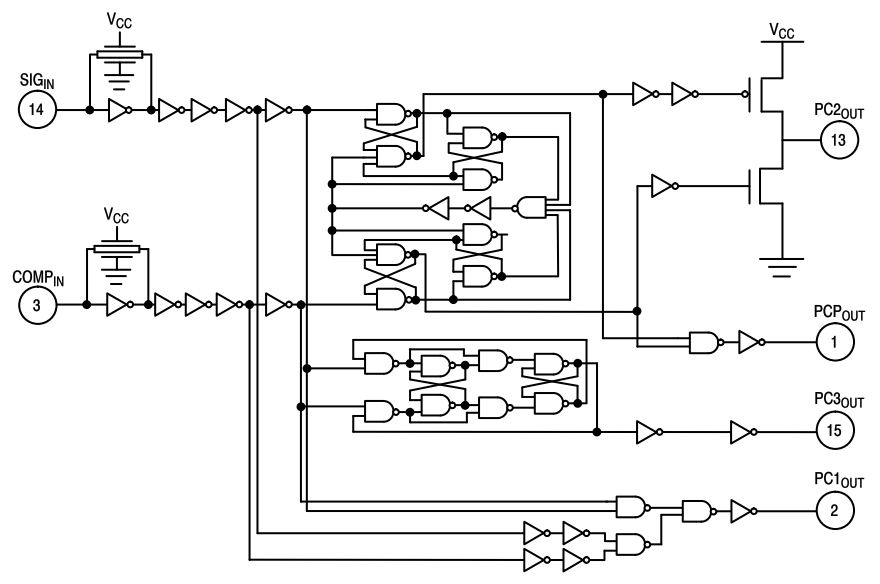
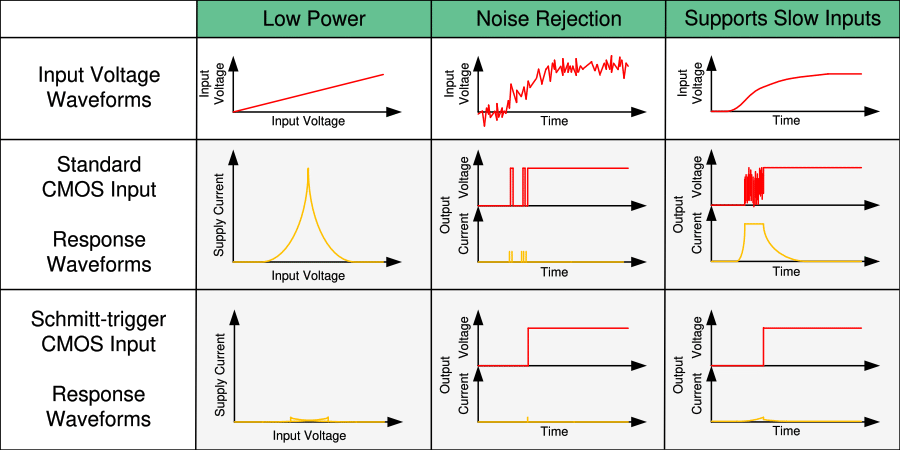
論理演算の基本は AND, OR, NOT ですが、CMOS IC にはそれに加えて現実の世界に対処するために、 バイラテラル(bilateral)スイッチ、シュミット・トリガー(Schmitt-trigger)入力、3ステート(three-state)出力があります。
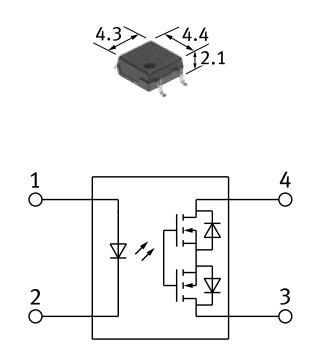
- バイラテラル・スイッチ
バイラテラルスイッチは双方向に電流を流すことができるスイッチで、 1組の N-MOS と P-MOS が並列に接続されてバイラテラル・スイッチの素子となっています。 これは、IC の内部で使われたり、アナログ信号を扱うアナログスイッチとして使われています。 (e.g. 74HCT4066, 74HCT4053)
- シュミット・トリガー入力
ある系の状態が過去の履歴に依存することをヒステリシス (hysteresis) と呼びます。 シュミット・トリガー (Schmitt trigger) は正帰還により入力の上り側と下り側で閾値が変わるヒステリシスを持つ電圧比較器で、 アナログ信号をデジタル信号に変換する能動回路です。
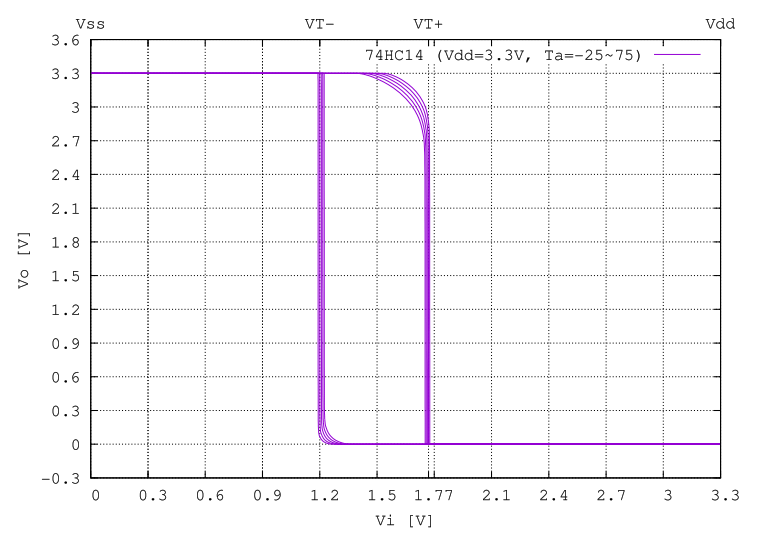
シュミット・トリガーを表すシンボルはこのヒステリシス特性の図に由来します。
- 3ステート出力
3ステート出力とは、その出力が H または L にドライブする状態とハイ・インピーダンス状態の3つの状態を持つものを言います。
データバスなど双方向にデータをやりとりするような箇所で使用されます。
3ステート出力を備えたバッファ IC の例 (74LVC2G125)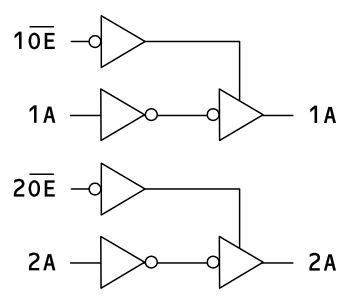
SR-FF (Set-Reset Flip-Flop)Transparent LatchOR 回路に帰還をかけてやると、セット・オンリー・フリップができます。
← 使えないやつ
当然このままですと使い物になりませんので、帰還路に AND ゲートを設けて帰還を断ち切ることができるようにします。 すると、リセット出来る(!)セット・リセット フリップ・フロップが出来上がります。これを NAND ゲートで構成すると下図のように 負論理入力、正論理出力の SR-FF になります。
D-FF (Delay Flip-Flop)SR-FF を1ビットの記憶素子として使うことを考えると、SR-FF には次の欠点があります。
(1) 2入力である。
(2) 入力の両方が同時にアクティブ(真)になった場合に不都合がある。
(3) 入力の変化が即座に出力に現れる。
(1),(2) の欠点を無くすために、セット入力とリセット入力をコンプリメンタリにし、
(3) の欠点を補うために、その入力にストローブ用ゲートを付け加え、
入力が安定している期間にストローブ信号により入力データを保持するようにしたものが 下図に示すトランスパレント・ラッチです。
JK-FF (JK Flip-Flop)記憶素子としてより使いやすく、クロック信号の立ち上がり('L'→'H' の変化)時に 入力データを保持すると同時に出力するようにしたものが、D-FF です。(立ち下がりで動作するものもあるが一般的ではない)
D-FF の動作説明
ゲート A, B 及び ゲート C, D はクロック信号により ゲートされる SR-FF になっており、SR-FF(A, B) と SR-FF(C, D) には入力の コンプリメンタリな信号が入力されています。
クロック入力が 'L' の間は、SR-FF(E, F) の両入力が 'H'(インアクティブ)になって いるため出力は変化しません。
入力データが 'H' である時を考えてみます。
このとき SR-FF(A, B) は、クロック信号により帰還路がゲートされているけれども、入力データに より ゲート A 出力がセットされている状態になっています。
同時に SR-FF(C, D) はセットもされず、クロックによりリセットされている状態になっています。
ここで、クロックが 'H' に変化したとすると
SR-FF(A, B) はセットされた状態になると同時に SR-FF(C, D) をリセットし続けることになります。
従って SR-FF(E, F) を SR-FF(A, B) がセットすることになり出力 Q に 'H' が現れ 、入力データが保持されることになりました。
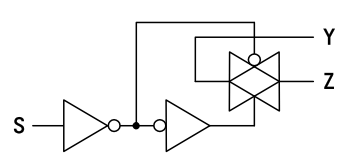
まとめると、クロックが 'L' のときには 出力フリップフロップ SR-FF(E, F) がデータを保持し、 クロックの 'L'→'H' の変化で 入力フリップフロップ SR-FF(A, B) または SR-FF(C, D) がデータを 取り込み、保持していると言えます。CMOS ロジック IC ならではの回路構成で、ラッチの構成用にバイラテラル・スイッチが活用されているものもあります。 (e.g. 74LVC1G79)
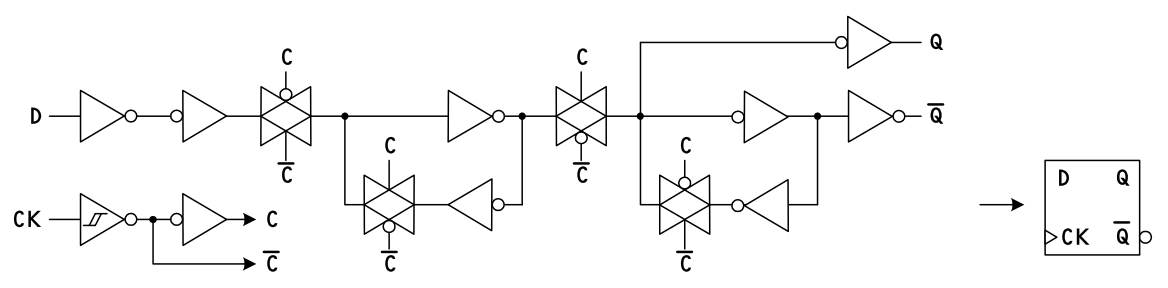
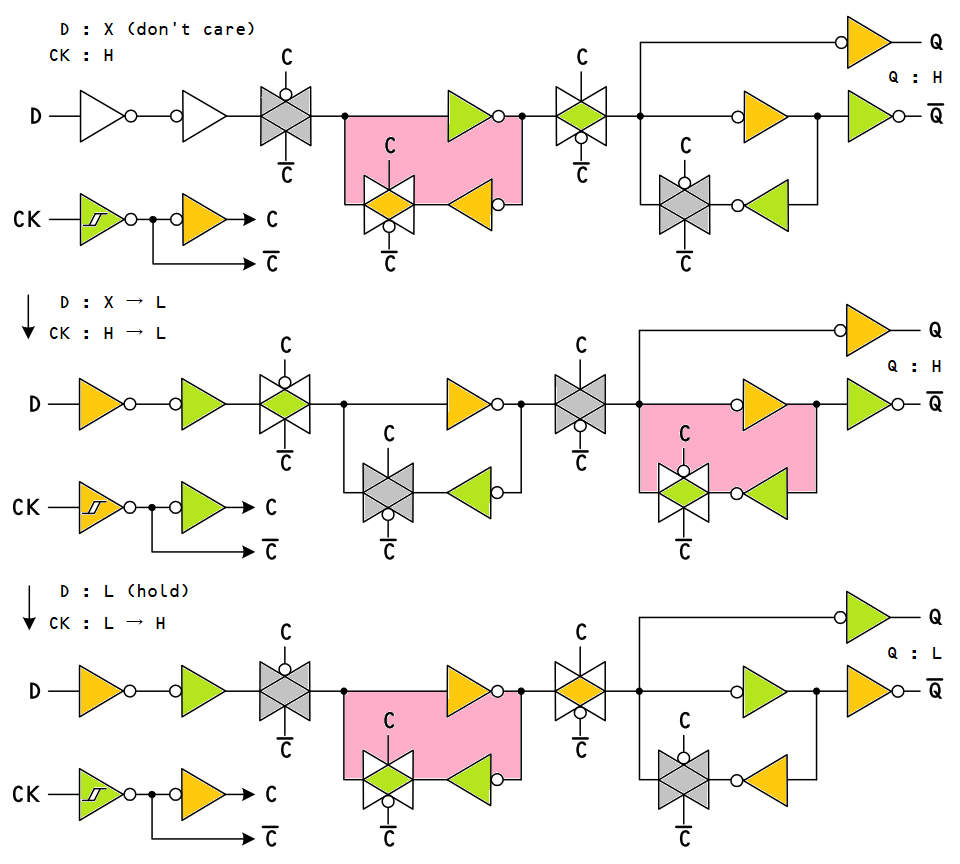
バイラテラル・スイッチを使った構成の D-FF の動作説明。
- 黄緑色のインバータは出力が L になっています。
- 橙色のインバータは出力が H になっています。
- 白色のインバータの出力は気にしなくて良いことを表します。
- 灰色のバイラテラルスイッチは遮断状態を表します。
- 中の菱形が黄緑色または橙色のバイラテラルスイッチは導通状態で、それぞれ L または H になっていることを表します。
- ピンク色の箇所は帰還ループが閉じていてデータを保持していることを表します。すなわちトランスパレント・ラッチとして働いています。
- クロックが H のときには、左側のプライマリ・ラッチ (primary latch) がデータを保持していて、それが出力されています。
- クロックが H → L のに変わると、右側のセカンダリ・ラッチ (secondary latch) にデータが保持されて、それが出力されます。
このとき、プライマリ・ラッチ側には次のデータが入力されています。- クロックが L → H に変わると、次のデータがプライマリ・ラッチに保持されて、それが出力されます。
SR-FF を使いやすくするために、クロックに同期して J でセット、K でリセットできるようにしたものが JK-FF です。
J, K 共に 1 のときにはクロックに同期して Q と Q が反転します。
JK-FF は、Q が 1 の時には K を、Q が 0 のときには J を選択するように、D-FF の入力にデータセレクタを 追加したものと等価です。
また、J, K にコンプリメンタリな入力データを与えるとその動作は、D-FF と同じになります。
個別の JK-FF の IC が使われることは稀ですが、ASIC や CPLD などの内部で シーケンサ(順序回路)を構成するときのモデルとして JK-FF はしばしば使われています。
JK-FF の名前の由来は、Q (Queen) を J (Jack) と K (King) が奪い合うからだそうです…と聞き及んでいましたが、実は次のようなことだそうです。
「ジェット推進研究所(JPL)のエンジニアであるリンドリー氏 (P. L. Lindley) が 1968 年 6 月 13 日付の電子技術誌 EDN 8 月号に寄稿した手紙によると、 1954 年の UCLA で行われたモントゴメリー・フィスター氏 (Montgomery Phister) のコンピューター設計の講義の中で、 2つの入力が '1' のときに出力状態が変化するフリップフロップが初めて取り上げられました。 当時ヒューズ・エアクラフト社 (Hughes Aircraft) のエルドレッド・ネルソン博士 (Dr. Eldred C Nelson) がそのフリップ・フロップのことを J-K と呼んでいました。 ネルソン博士は、J と K が「無害で良い文字」であることから、J と Kをシステムの各フリップフロップのセットとリセットの入力として使用することにしました。 ネルソン博士は、1953 年 9 月 8 日に申請されて 1958 年 9 月 2 日に認可されたアメリカ合衆国の特許 US2850566A の中で、j-input, k-input という言葉を使っています。」
"High-speed printing system" US2850566A より一部抜粋

これまでに述べたロジックまとめてユーザーでプログラム可能にしたデバイスとして、 CPLD (Complex Plogrammable Logic Device) や FPGA (Field Programmable Gate Array) が作られています。 下の図はやや古典的な Altera(現 Intel) の CPLD のマクロセルの例です。 マクロセルとは1つの出力を構成することのできるプログラマブルな論理セルのことです。 このようなデバイスをプログラムするために、HDL(ハードウェア記述言語)が用いられています。
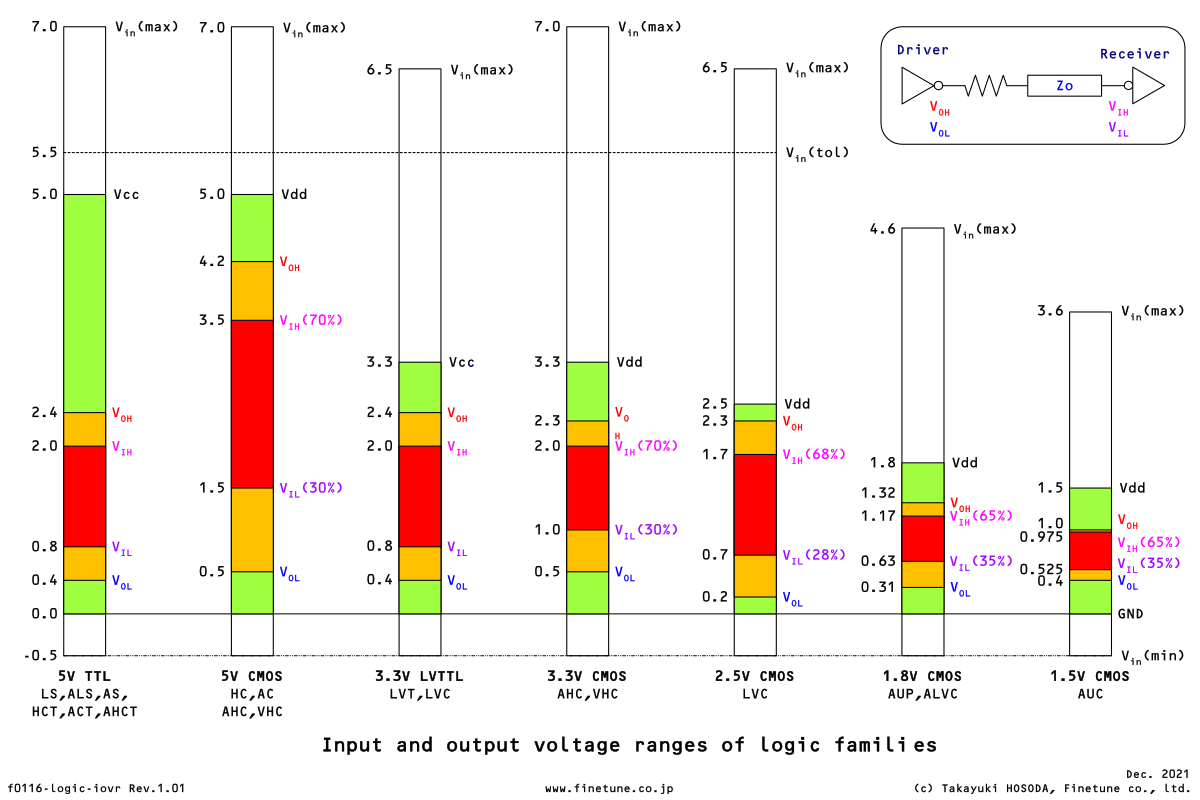
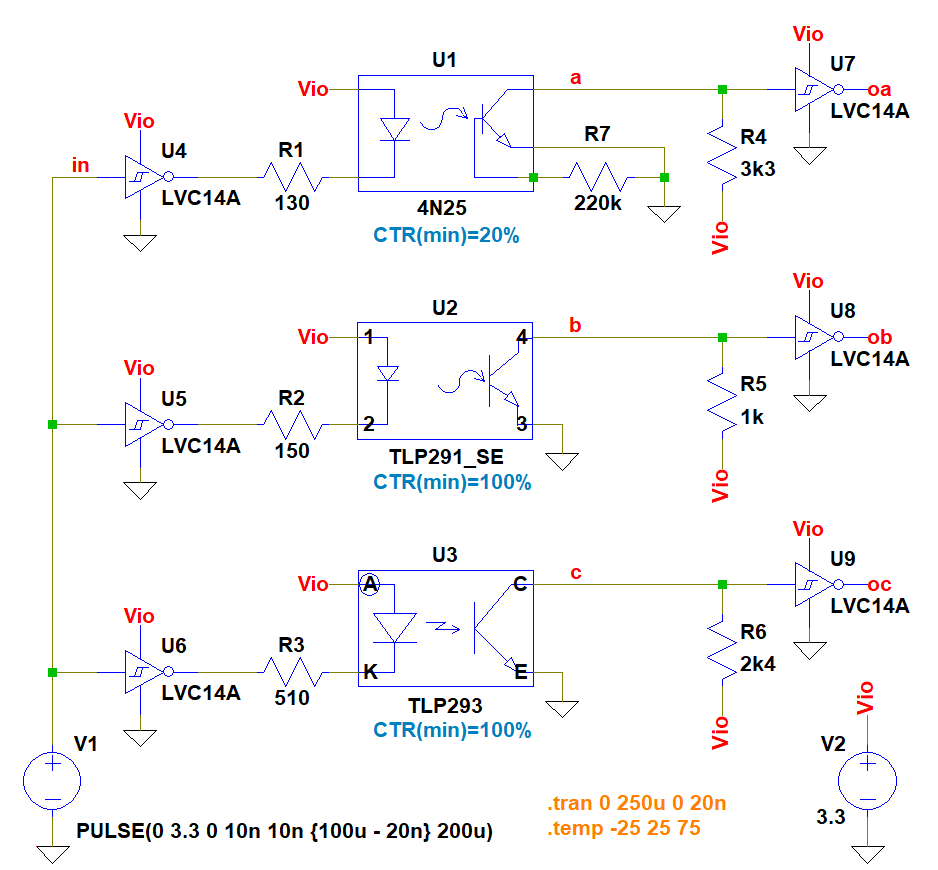
➡ LV-CMOS の直列終端の例
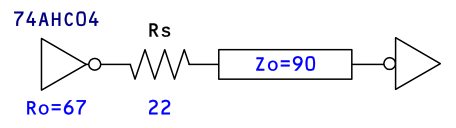
⚠️電気信号を扱う全ての IC や LSI の電源端子には、一般に良くパスコンと呼ばれるデカップリング・キャパシタが必須です。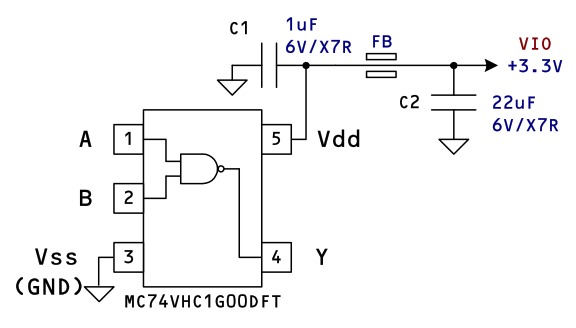
ある LSI メーカーによるとハードウェア的トラブルの 99 % 近くはパスコン不足もしくは不適切なパスコンに起因するものだそうです。 小規模なロジック IC では、パスコンに 100nF 〜 1uF 程度の MLCC (Multi Layer Ceramic capacitor) が多用されています。 パスコンは自身の安定動作のためにも必要ですが、不要輻射を低減するためにも IC の(電気的な)極近傍に配置することが重要です。 高速な CMOS ロジックでは、スイッチング時のスパイク電流や各所の容量を充放電するのに、パスコンの電荷が再分配されていると言っても過言では有りません。そしてその急峻なスパイク電流が流れる面積が大きいと不要輻射も大きなものとなるからです。
⚠️電源のパスコンに固体タンタル・コンデンサを使ってはなりません。故障モードの 90 % 以上が短絡で発火に至ることも稀では有りません。 ヒューズ入りの固体タンタル・コンデンサでは発火を防げる場合もありますが、RoHS 指令以降ヒューズ内蔵の固体タンタル・コンデンサも姿を消しました。セラミック・キャパシタは短絡しても発火することは有りません。 IC 周辺の電源の大容量のパスコンは 22μF 程度の大容量 MLCC(積層セラミックキャパシタ)を複数個使用し、共振防止にはチップ・フェライトでダンピングするのが現在の主流です。
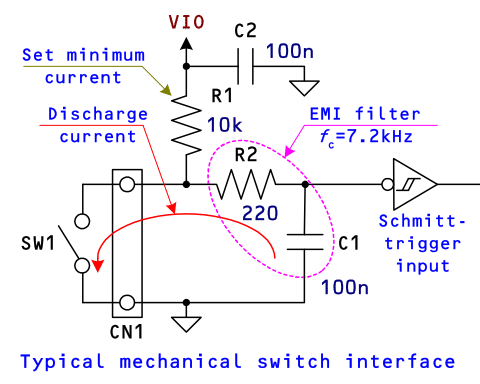
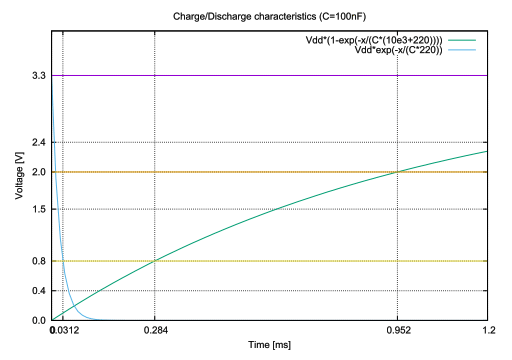
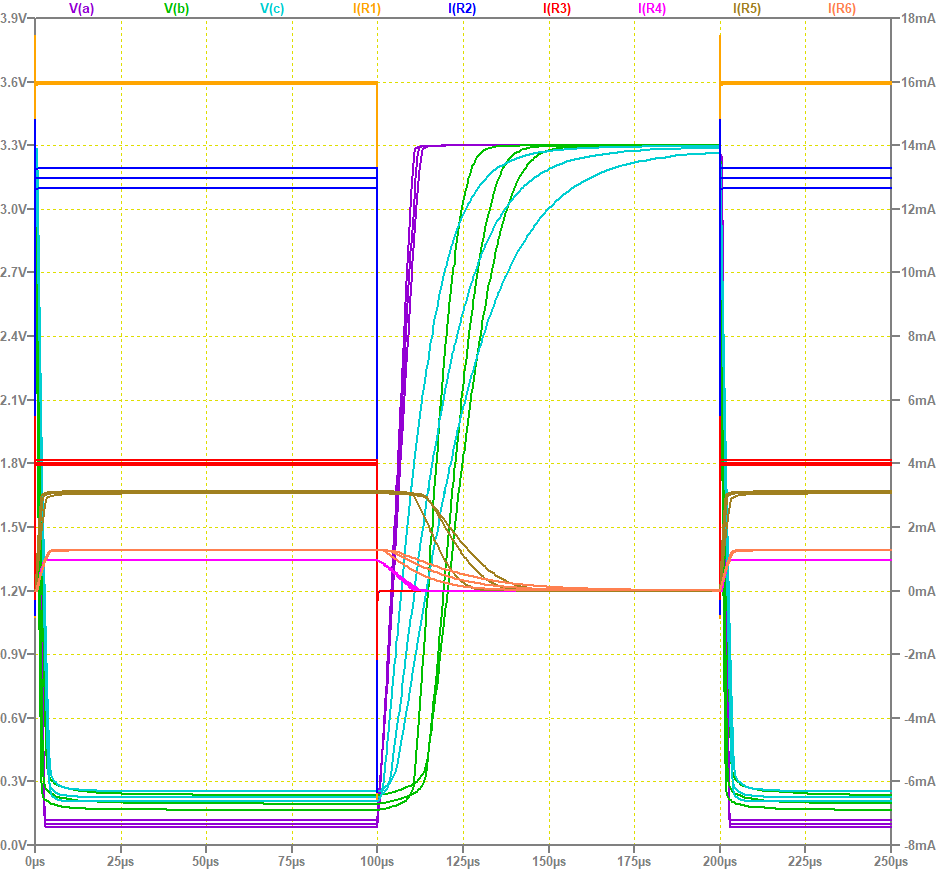
放電時は C1 R2 の時定数で放電されるため、シュミット・トリガー入力の VTL に達するまでの立ち下がりは約 30 μs と高速ですが、立ち上がりは C1 (R1 + R2) の時定数で充電されるため、約 1ms と低速です。
フリップ・フロップの応用回路例として、デジタル・デバウンス回路を紹介します。 デジタル・デバウンス回路はスイッチやリレーなどメカニカルな接点からの信号を受け取る箇所に使われる回路で、 接点が特にオフからオンになる過渡時に機械的な跳ね返りや酸化皮膜などの影響で断続的になるのを除去する回路です。 静電気の放電や外来雑音のスパイクによる誤入力を防ぐ役割もあります。
この回路では、外部スイッチの信号を EMI フィルタで高周波や静電気の影響を低減した後、 フィルタでなまった波形をシュミット・トリガー・インバーター (e.g. 74HC14) で波形整形しつつ正論理に変換して デジタル・デバウンス回路に入力しています。
デジタル・デバウンス回路では、外部からの信号 D をただ1つの D-FF で受け取り、 それを直列接続のもう2つの D-FF に入力します。この3つの D-FF の出力が全て 1 になったとき、 すなわち、クロックの3回分の時間連続して入力として 1 がサンプリングされたとき、 次のクロックでに次段の JK-FF がセットされます。 同様に3回連続して 0 がサンプリングされたときに JK-FF はリセットされます。
クロックの周波数(あるいはクロック・イネーブルの間隔)は想定されるバウンスが収まる時間と同程度に 設定します。サンプリング間隔の合間に外来雑音の短いスパイクがあったとしても、 サンプリングされないため、この影響を除去することができます。
スイッチ・インターフェース部の補足ですが、R2, C1 で EMI フィルタを構成し、中波から UHF の EMI や 静電気の放電(ESD, Electro Static Discharge)の影響を低減します。ここで、R2の値はスイッチ Sw がオンになったときに C1 の放電電流 がスイッチの定格電流を超えないようにR2の値を設定してします。 小信号スイッチの最大電流は 50 mA 程度のものが多いため VIO が 3.3 V として ISw(max) = 3.3 / 220 = 15 mA としています。
D-FF はクロック入力のエッジに対して、入力データが変わってはいけない時間が決められており、 クロックの前の安定しているべき時間がセットアップ時間 tsu、クロック後に安定しているべき時間がホールド時間 th です。
ところが外部からの信号はクロックに対して非同期ですので、セットアップ時間の違反が起こることがあります。 このようなときには、D-FF の出力が安定するのに長い時間を要することがあります。 このような状態をメタ・ステーブルと呼び、非同期の信号を扱うときには常に考慮しなければなりません。 メタステーブル対策的に、外部からの信号は「ただ1つの D-FF で受ける」のが鉄則と言えます。
最近では、雑音が多かったり鈍った波形の信号とのインターフェース用に、入力がシュミット・トリガーになっている D-FF (e.g. SN74HCS174) も発売されています。
デジタル・デバウンス回路が個別のロジック IC で構成されることは稀で、一般的には FPGA (Field Programmable Gate Array) の一部、 あるいは MCU (Micro Control Unit) のソフトウェアの処理の一部として組み込まれます。 (c.f. ハードウェア的プログラミングのすすめ)
デジタル・デバウンス回路も回路図で書くと複雑に感じますが、論理式で書くと簡単です。
従って、通常は機械接点インターフェースとしてのハードウェア的には、プルアップ抵抗とフィルタとシュミット・トリガー入力があれば良いことになります。Q1 := D; Q2 := Q1; Q3 := Q2; SW := (!SW & (Q1 & Q2 & Q3)) #( SW & (Q1 # Q2 # Q3));但し、ここではクロックに同期した D-FF への入力を := で表すこととします。
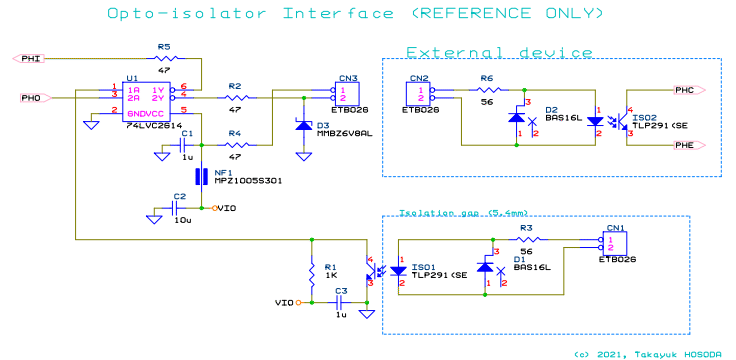
シミュレーション用回路図
過渡特性
シミュレーション用回路図
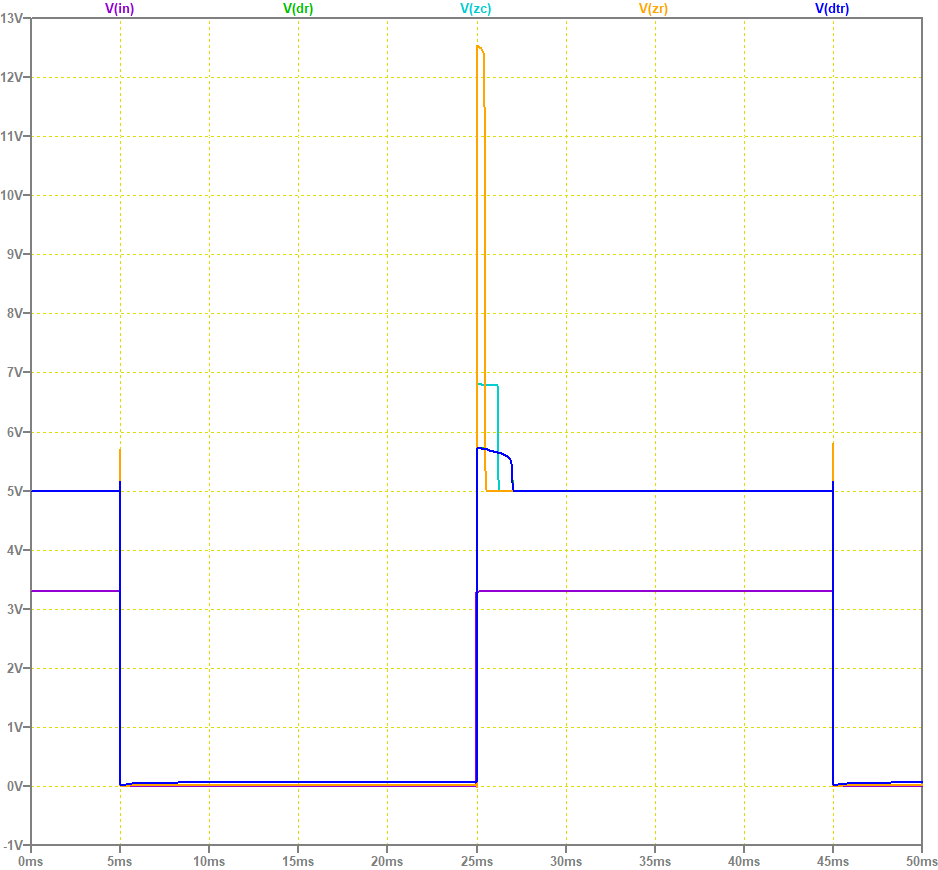
過渡特性
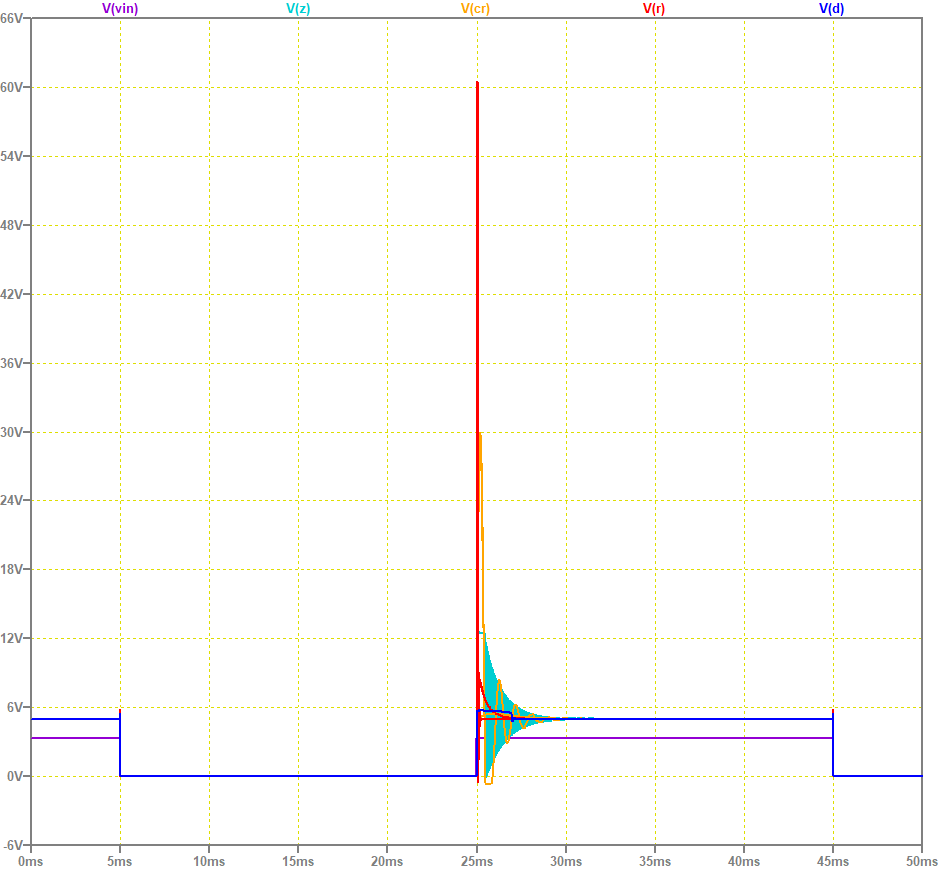
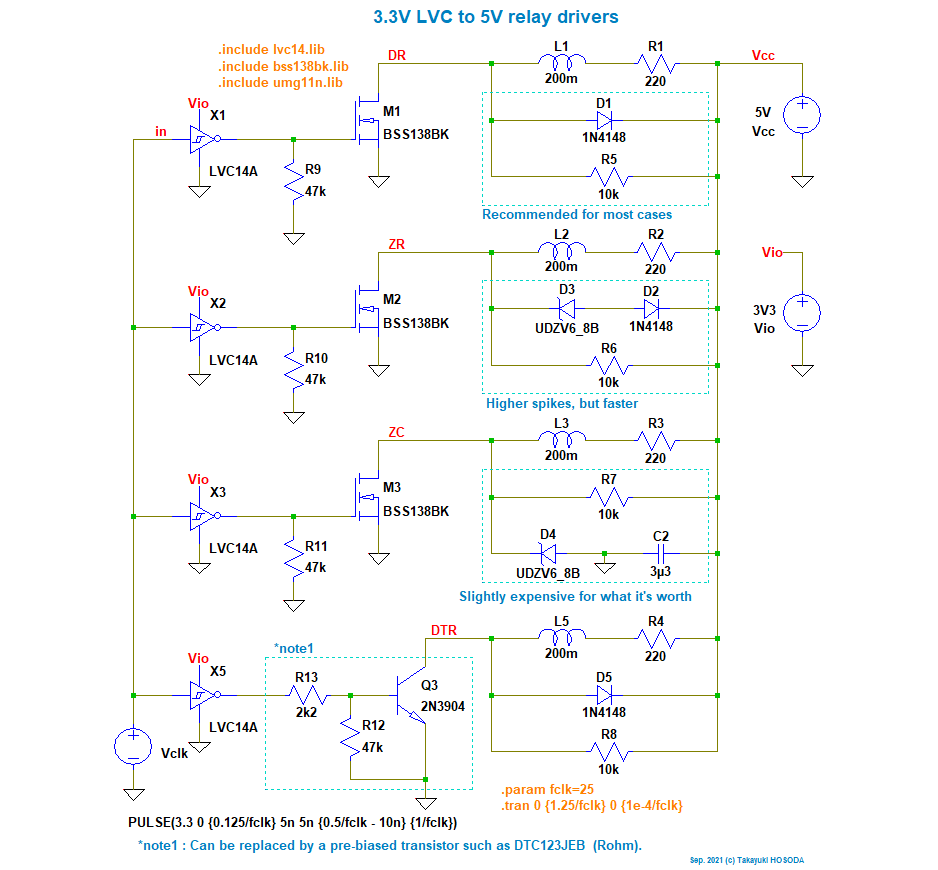
シミュレーション用回路図
実際のリレーのコイルのインダクタンスと抵抗値の例 (非動作時)
20211011T1720, 26.0 ℃, Teruyuki KUWAHARA, Teruyuki KUWAHARA, Finetune co., ltd. Hioki IM3570 + L2000, Vm = 0.1 V, Fm = 10 Hz FTR-B3ZA4.5Z : 149.0 Ω + 34.8 mH FTR-MYAA005D : 217.8 Ω + 200.2 mH FTR-LYCA005V : 147.1 Ω + 168.4 mH 動作時のインダクタンスは非動作時の約2倍となる製品が多いようです。
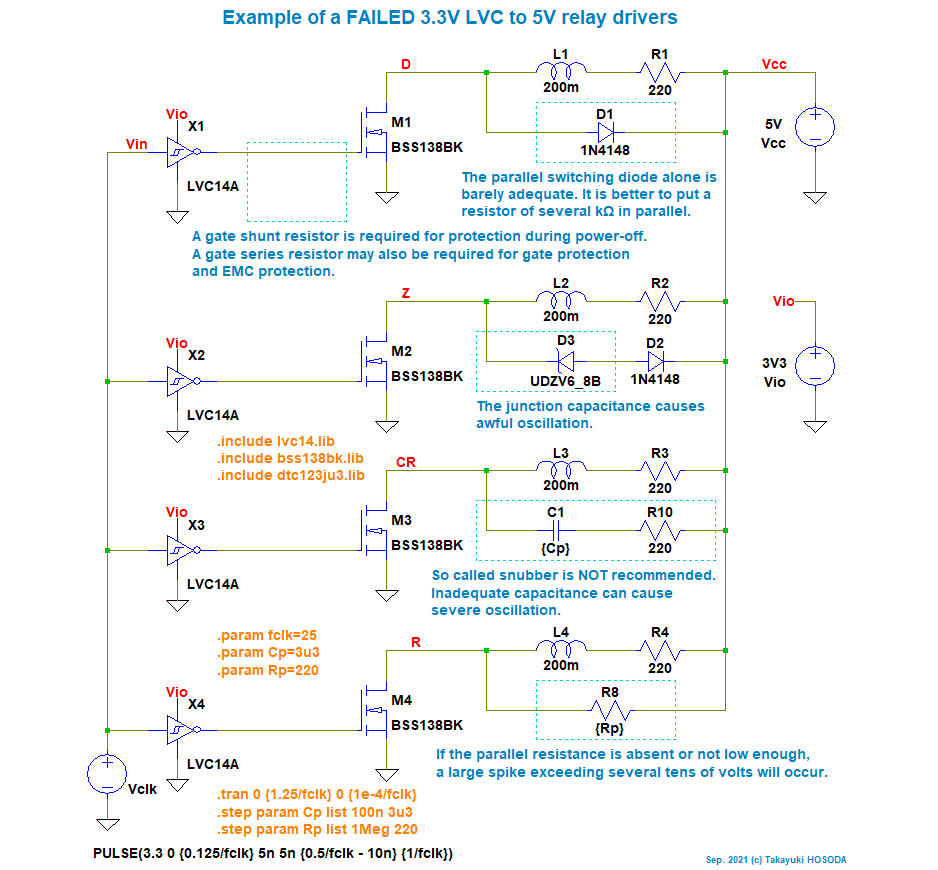
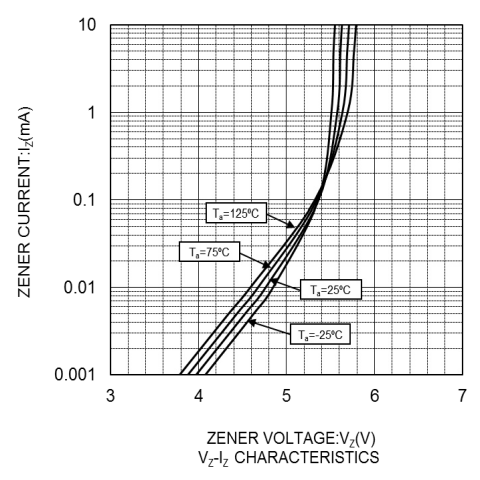
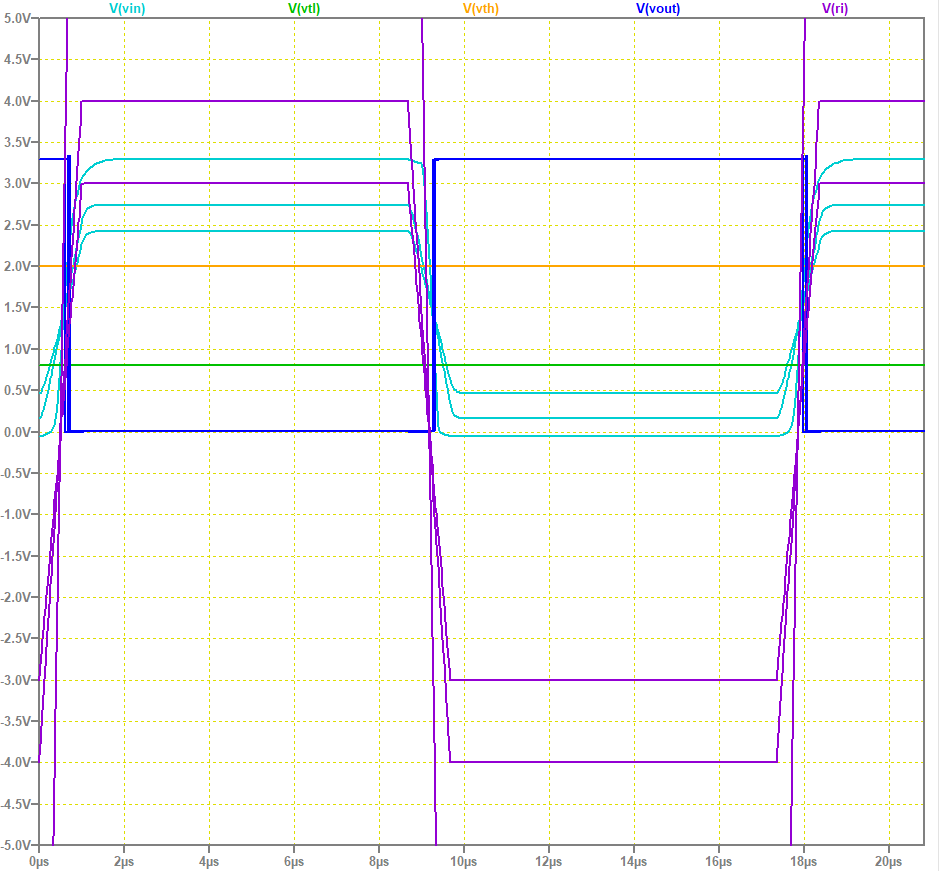
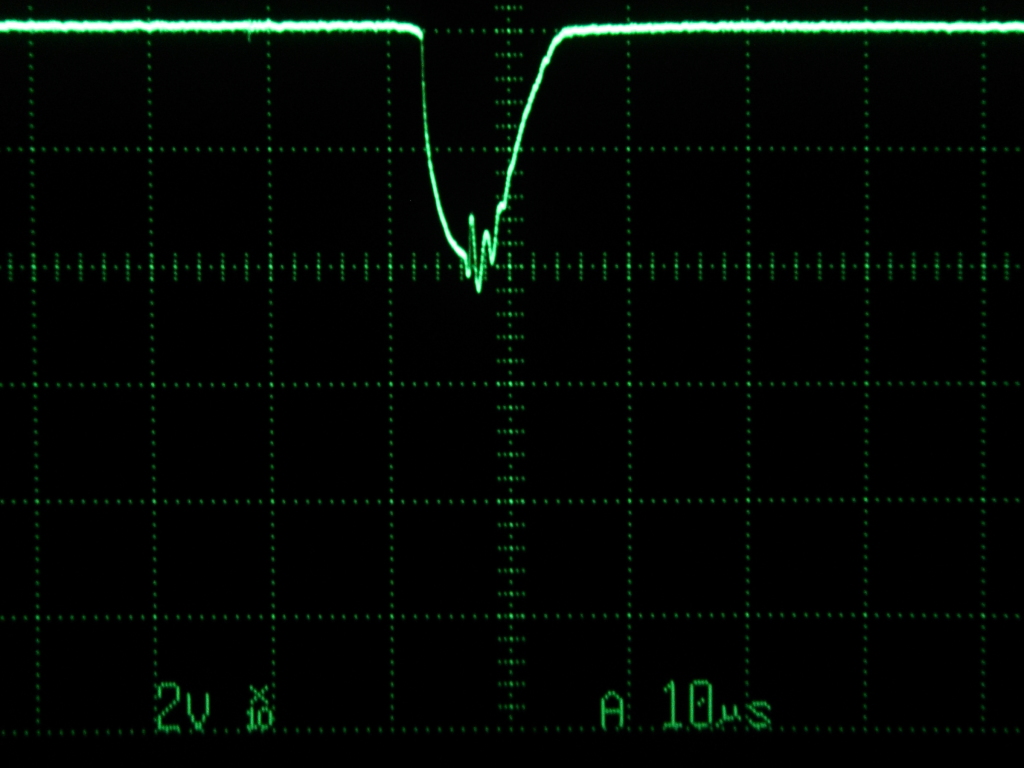
M2 の出力 Z では、M2 がオンの間に L2 にエネルギーが蓄えられますが、 M2 がオフになったときにこのエネルギーの一部は D3, D2 で消費されますが、 D3 がオフになったときに D3 の接合容量と L2 で周波数の高い振動を引き起こす恐れがあります。 これは、電子部品の故障や雑音の原因となります。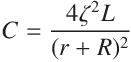
ζ : ダンピング・ファクタ
TBD62083AFNG (Toshiba), 2.5V-CMOS input, 8-channel DMOS FET array, 50V, 100mA, N-ch output従来品に対するアドバンテージ
内部構成 ( 1 回路分)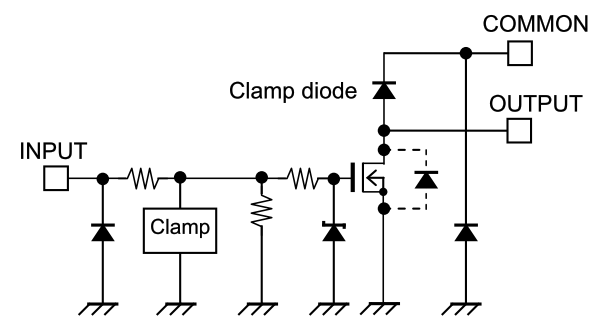
諸元抜粋
TBD62083A : Iin≦0.10mA@2.5V, Ron≒2.0Ω@Iout=0.2A, Ton/off=0.4/0.8us
諸元比較
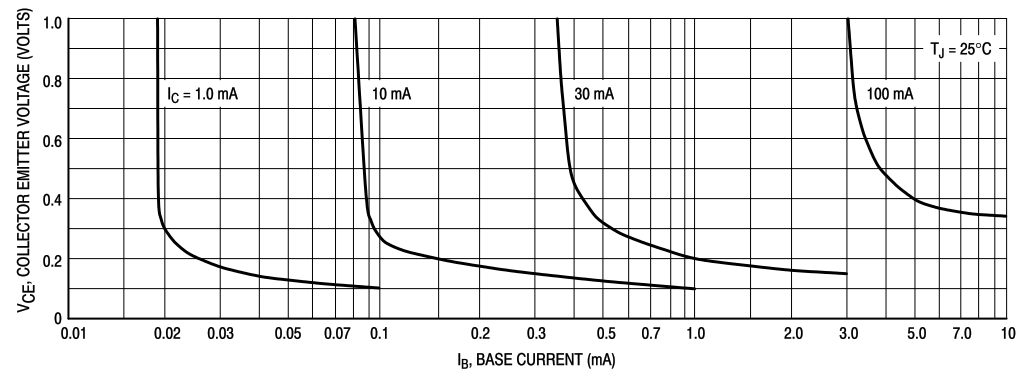
TD62083A : Iin≦0.35mA@5.0V,Vce≒1.3V @Iout=0.2A,Ton/off=0.1/0.2us入力電流
TBD62083A : Iin≦0.10mA@2.5V,Ron≒2.0Ω@Iout=0.2A,Ton/off=0.4/0.8us
従来品の出力素子のダーリントントランジスタは電流駆動素子であるため、特に大電流時に低めの出力飽和電圧を得るためには、 比較的大きな入力電流が必要となり、3.3 V 系のロジック IC では入力電流不足となって不適合となる場合がありました。 TBD62083Aでの出力素子の DMOS FETは電圧駆動素子であるため、入力電流が約 0.1 mA と少なくて済み、3.3 V 系のロジックICに適合します。 総出力電流が問題となる多ピンの LSI 等への直接接続にも適し,また EMC 対策的にも有利となります。出力電圧
従来品では出力がダーリントントランジスタであるために本質的に避けられない 0.9 V 以上もある大きな出力飽和電圧が問題となることがありました。 例えば 5 V 系のリレーを 5 V 電源で駆動するのには駆動電圧不足となるため適していませんでした。 TBD62083A では、出力素子の DMOS FET の出力オン抵抗が低く,出力電圧が低減出来るようになりました。発熱
従来品では出力部の損失に起因して、例えば 0.2 A 程度の負荷においても約 0.22 W の損失で 4ch 分でデバイスの許容損失の 0.96W (SOP18)に近くなるために、熱的に 8 ch のチャネル数を活かすことが出来ない場合がありました。 TBD62083A では出力オン時の消費電力が同 80mW 程度と少なくなったため、8ch 全部を利用しやすくなりました。
TBD62783AFNG (Toshiba), 2.5V-CMOS input, 8-channel DMOS FET array, 50V, 100mA, P-ch output
内部構成 ( 1 回路分)
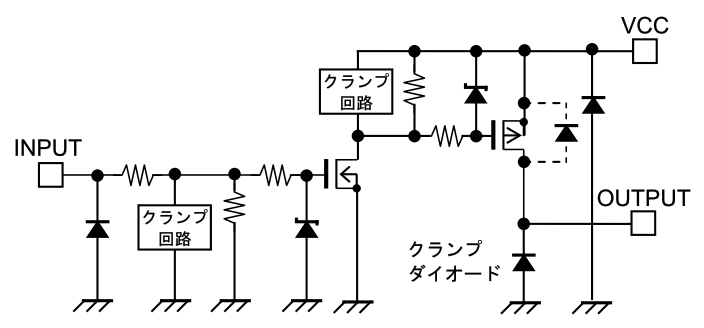
諸元抜粋
TBD62783A:Iin≦0.10mA@2.0V,Ron≒1.6Ω@Iout=0.2A,Ton/off=0.15/1.8us
DMOS-FET アレイ TBD62083A の応用回路例 (参考)
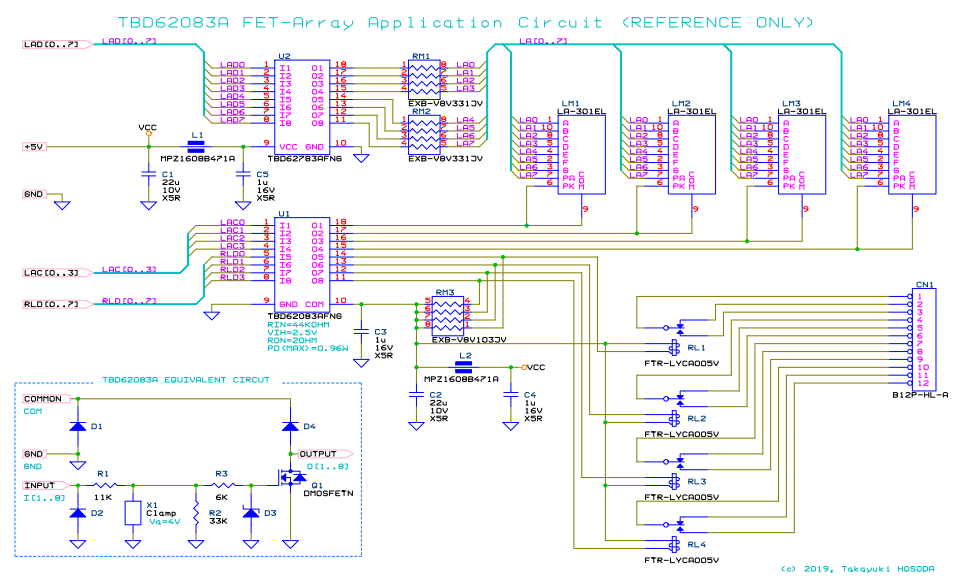
U1:TBD62083AFNG の半分を 5V駆動 6Aクラス のリレーの制御に使用し、もう半分を 4桁の 7セグメントLEDのダイナミック点灯に使用しています。
U2:TBD62783AFNG は TBD62083AFNG の姉妹品で電流ソースタイプのものです。
U1 は 3.3V 系の CMOS ロジックIC や FPGA から駆動されることを想定しています。
C3 は U1 用の C5 は U2 用のデカップリング用キャパシタです。
C2, L2, C4 と C5, L1, C1 でそれぞれ EMCフィルタを構成しています。
U1, U2 は短絡保護回路を含まないため、短絡に対して積極的にはヒューズや電流制限素子での対策が必要ですが、
出力短絡の可能性の低いこの回路例では万一の場合には L1, L2 がヒューズ的に働くことを期待して他の保護素子は用いていません。
RM1, RM2 は LM1〜LM4 の LEDの電流制限抵抗ですが、U2 出力の直近に配置されて直列終端的にも働き不要輻射を低減します。
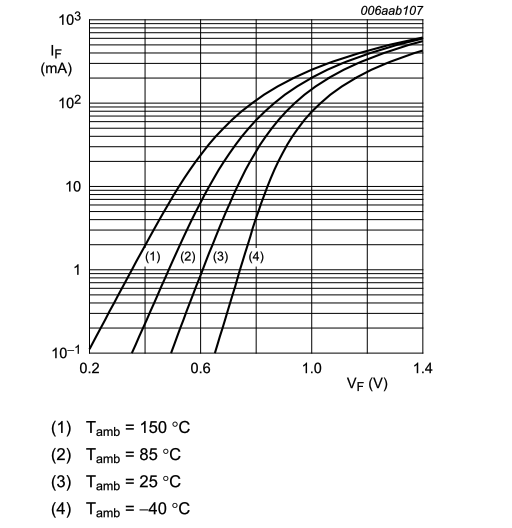
パリティ・チェック反転2連送パリティ・チェックは一番簡単な誤りチェックです。 データにパリティ・ビットを付け加えて符号とし、符号中の 1 の数が偶数(または奇数)になるようにパリティ・ビットを決めます。 このパリティ・ビットにより符号のハミング距離が 2 となり 1-bit 誤りの検出が可能となります。 符号中の 1 の数が偶数になるようにパリティ・ビットを選んだものを偶数パリティ (even parity) と言い、 奇数のものを奇数パリティ (odd parity) と言います。 偶数パリティはデータ中の 1 を mod 2 で加算した結果とも言えるし生成多項式 X + 1 で割った余りとも言えます。
例:5-bit のデータが 10110 の場合
- パリティ生成: X + 1 で割った余り
10110 データ 11 ----- 1110 11 ---- 10 11 -- 1 偶数パリティ- 符号生成:データの末尾にパリティ・ビットを追加し送信符号とする
101101 送信符号
- 受信誤りがない場合
余りが 0 → 誤り無し101101 送信符号 000000 誤り無し ------ 101101 受信符号 11 ------ 11101 11 ----- 101 11 --- 11 11 -- 0
- 受信符号に 1-bit 誤りがある場合の例
余りが 1 → 誤り有り101101 送信符号 00X000 誤り ------ 100101 受信符号 11 ------ 10101 11 ----- 1101 11 ---- 1CRC (Cyclic Redundancy Check, 巡回冗長検査)反転2連送はデータにデータを反転したものを付け加えて符号とします。
例:8-bit のデータが 1011 0010 の場合
反転2連送は簡単な構成でデータ長以下のバースト誤りの検出ができます。
またデータが 0 や 1 に固着した誤りの検出もできます。
- 符号生成:データと反転データ
- 受信誤りがない場合
データと反転データ部の XOR が全ビット 1 → 誤り無し1011 0010 0100 1101 送信符号 0000 0000 0000 0000 誤り無し ------------------- 1011 0010 0100 1101 受信符号 0100 1101 --------- 1111 1111
- 受信バースト誤りがある場合
データと反転データ部の XOR に 0 のビットがある → 誤り有り1011 0010 0100 1101 送信符号 0000 0X0X X0XX 0000 7-bit バースト誤りあり ------------------- 1011 0111 1111 1101 受信符号 1111 1101 --------- 0100 1010誤り訂正CRC は巡回符号に基づいた誤り検出符号の一種です。 データ列を決められた n + 1 ビットの生成多項式で割った余りをデータに付け加えて符号とします。 チェック・ビットが n-bit の CRC は符号中の n-bit 以下のバースト誤りを検出することができます。 生成多項式により各種の CRC がありますが、よく使用されるものには次の辺りです。
- CRC-8-CCITT : x8 + x2 + x1 + 1 (0x107)
- CRC-8-Dallas/Maxim : x8 + x5 + x4 + 1 (0x131)
- CRC-8-Bluetooth : x8 + x7 + x5 + x2 + x + 1 (0x1a7)
- CRC-16-CCITT : x16 + x12 + x5 + 1 (0x11021)
- CRC-16-IBM : x16 + x15 + x2 + 1 (0x18005)
- CRC-32 (IEEE-802.3) : x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 (0x104c11db7)
- CRC-32C (Castagnoli, RFC 3720, iSCSI) : x32 + x28 + x27 + x26 + x25 + x23 + x22 + x20 + x19 + x18 + x14 + x13 + x11 + x10 + x9 + x8 + x6 + 1 (0x11edc6f41)
CRC の計算における生成多項式での剰余を求める計算は、 シリアルデータの場合は下図のようなリニア・フィードバック・シフト・レジスタで簡単かつ高速に求められるため、 固定長やフレーム構造を持つシリアルデータの誤り検出に多用されています。
生成多項式 x8 + x5 + x4 + 1 での除算回路例Data の入力が終わったときのレジスタの内容が剰余となり、これを CRC とします。
➡ 2元 BCH 符号及びバースト誤り訂正符号 — 生成多項式一覧及び誤り訂正デモンストレーションとプログラム例(C, JAVA)
➡ Charmsec® 誤り訂正文字化符号 — デリミタ対応・スーパーデータも使える
作りたい機能があれば論理式や状態遷移等を考えて設計し、論理合成します。論理合成は今は HDL コンパイラの仕事です。 人間の仕事は、実現したいことを考えることと、信頼できる装置を実現することと、周りに迷惑な雑音を発生させないことです。 人は割と簡単に死ぬ脆弱な生き物です。 たかが電子装置のせいで火災や事故が起きたりして尊い命が失われないようにすることが何よりも大切です。 便利さや機能にとらわれたり、納期に追われたりしておろそかにしがちですが、 デバッグや問題解決よりも問題を発生させないための設計に時間を使いたいものです。

![[Mail]](/~lyuka/images/mail.gif)

 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.