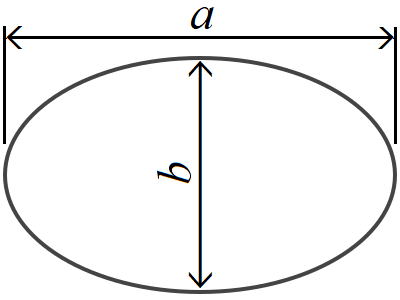
The calculation is performed using the relationship between
Complete Elliptic Integrals of the Second Kind and the AGM (Arithmetic Geometric Mean).
The approximation of Ramanujan's elliptic perimeter is also calculated.
Some reference values of accurate (to 65 decimal digits) perimeters by WolframAlpha.
a = 1, b = 1 : 6.2831853071795864769252867665590057683943387987502116419498891846... = 2π (exact) a = 2, b = 1 : 9.6884482205476761984285031963918294119539183978866008250831163524... a = 5, b = 1 : 21.010044539689000944699164588473738912894812339134152623096835657... a = 10, b = 1 : 40.639741801008957425577931011816563791313052134504059403405927819...
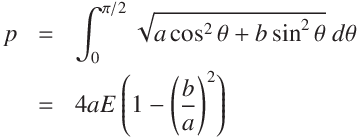
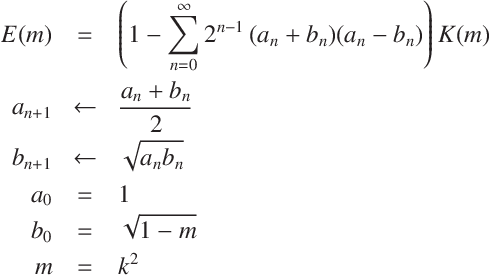
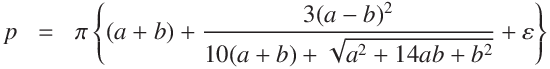

![[Mail]](/~lyuka/images/mail.gif)

 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.