Exponent of Lambert W function for HP 42S

for HP 42S
e^W - Exponent of Lambert W function

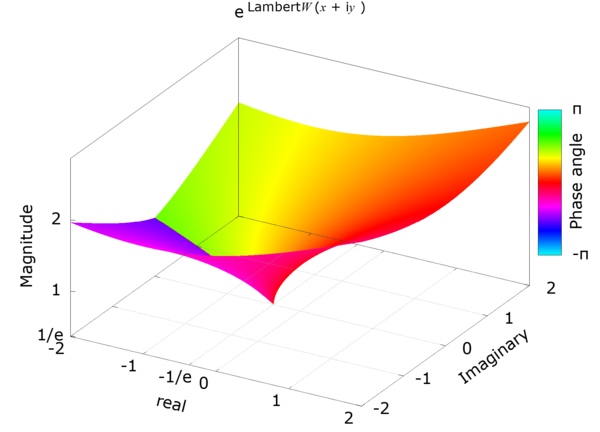
exp(LambertW(x+iy))

From the relation below, the Lambert W can be calculated by using e^W — the exponent of Lambert W — as ln(e^W(x)) or x / e^W(x).

$W(x) = \frac{x}{\mathrm{e}^{W(x)}} = \ln\big(\mathrm{e}^{W(x)}}\big\,)$

e^W₀(x) — the exponent of the principal branch of the Lambert W function W₀(x) — can be calculated by using Newton-Raphson method,

$y_\mathrm{n+1} \leftarrow y_\mathrm{n} - \frac{y_\mathrm{n}\ln(y_\mathrm{n}) - x}{\ln(y_\mathrm{n}) + 1}$

or equivalent and simpler, but slightly less accurate recurrence formula below.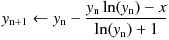

$y_\mathrm{n+1} \leftarrow \frac{y_\mathrm{n} + x}{\ln(y_\mathrm{n}) + 1}$

If you try to find e^{W₀ (x)} for x that is very close to -1 / e i.e. singularity, with Newton-Raphson method, it would go bad from a convergence point of view. So, it is desirable that the approximation error of the initial value is asymptotic to 0 at -1 / e. For that reason, I chose the following formula as an approximate expression that gives the initial value.

$y_0 = \frac{1}{\mathrm{e}} + \sqrt{\frac{2}{\mathrm{e}} \, \bigg(\frac{1}{\mathrm{e}} + x\bigg)} + 0.3 \,\bigg(\frac{1}{\mathrm{e}} + x\bigg)$

Instead of the coefficient of 0.3 in the formula above, it can be "e - √2 - 1" which makes zero error at x = 0, or "1 / 3" from Puiseux series, but 0.3 is quite good enough for this purpose.

It's nice to be able to handle complex numbers easily with 42S, and thanks to SQRT √ in this equation, 42S can automatically get the complex y₀ from x less than -1 / e.

eW - Rev.1.4 (Oct. 6 2020)

eW - calculate e^{W₀ (x)}
     Rev.1.4 (Oct. 6 2020)
     (c) Takayuki HOSODA, Albert Chan, Werner Huysegoms

Input   X : x 

Output  Z : x
        Y : e^{W₀ ( x )} 
        X : e^{W₀ ( x )}

Recurrence formula (Newton method) :

   

Initial approximation :


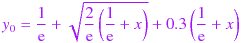
00 { 53-Byte Prgm }
01▶LBL "eW"
02 0.3
03 -1
04 E↑X
05 RCL+ ST Z
06 STO× ST Y
07 STO+ ST X
08 LASTX
09 STO+ ST Z
10 ×
11 SQRT
12 +
13 X<>Y
14 +/-
15 X<>Y      # Initial value
16▶LBL 01
17 X=Y?      # Convergence check
18 RTN
19 STO ST Y
20 LN
21 1
22 +
23 R↑
24 RCL+ ST Z
25 X<>Y
26 ÷        # Newton-Raphson method
27 -
28 STO× ST X
29 LASTX
30 STO+ ST Y
31 GTO 01
32 .END.

Download 'eW-1.4.raw' for Free42 or DM42

Acknowledgments

Thanks to Werner of the hpmuseum forum for his advice on reducing the code by several bytes :-)
Thanks to Albert Chan of the hpmuseum forum for extending the code to accept complex input :-)

Examples (calculated by WolframAlpha)

DBL_MAX := 1.7976931348623157E+308
M_E     := 2.7182818284590452354
M_1_E   := 0.36787944117144232160
exp(lambertw(2.7182818284590452354)) ≈ 2.718281828459045235380143735676331
exp(lambertw(1 -2 * I)) ≈ 1.963022024795710615403657609352963 - 1.157904818620494603558662182506434 * I
exp(lambertw(1)) ≈ 1.763222834351896710225201776951707
exp(lambertw(I)) ≈ 1.219531415904638290761849581476316 + 0.79276048053626614951364590110420540 * I
exp(lambertw(0)) ≈ 1
exp(lambertw(-0.36)) ≈ 0.44660340471508799282336704382334493
exp(lambertw(-0.36787944117144232160)) ≈ 0.3678794411714423215940316935486145 + 5.738837742185627565654911654550658e-11 * I
exp(lambertw(-0.37)) ≈ 0.36717276900330783668441776919458851 + 0.039505937830337093378017782321873547 * I
exp(lambertw(-1)) ≈ 0.16837637908722291055702904019641980 +0.70775418878472761647284589307651624 * I
exp(lambertw(-1.78)) ≈ -0.059913754741825131012618862446014644 + 1.0916761607000236604411601478529583 * I
exp(lambertw(-6 + 8 * I)) ≈ 0.5264016089780162506063934272535399 + 4.672167782982315920355097205014711 * I
exp(lambertw(-1e40+ 1e40 * I)) ≈ -1.105839096727961926761463409591397e38 + 1.166002733393463635466614023256946e38 * I
exp(lambertw(1e99)) ≈4.493356750426821622552404615870473886e96
exp(lambertw(DBL_MAX / 2048)) ≈ 1.261879051192686334779289930192228092e302
exp(lambertw(DBL_MAX / 1024)) ≈ 2.521249396109343724237771081311131912e302
exp(lambertw(DBL_MAX / 1024 * (1 + I))) ≈ 2.522830663716190666378256473298873041e302 + 2.517156775366979709124816162156298866e302 * I
exp(lambertw(-DBL_MAX / 1024 * (1 + I))) ≈ -2.511457441673898564070201945759970065e302 + 2.528478934471466911545439081960013883e302 * I
exp(lambertw(-DBL_MAX / 1024)) ≈ -2.521198257475903786620327462027548275e302 + 1.135883576664975088461252871876537019e300 * I
exp(lambertw(DBL_MAX / 512)) ≈ 5.037491337606633333196094048616224613e302
exp(lambertw(DBL_MAX / 256)) ≈ 1.006498762266630559657258456161750187e303
exp(lambertw(DBL_MAX / 128)) ≈ 2.011002473565593500923176245177799597e303
exp(lambertw(DBL_MAX / 4)) ≈ 6.403475847440308183677482911752527470e304
exp(lambertw(DBL_MAX / 2)) ≈ 1.279433384662740296920509547057383184e305
exp(lambertw(DBL_MAX)) ≈ 2.556348163871690389301867464319449906e305
exp(lambertw(-DBL_MAX)) ≈ -2.55629732717928176150546584430620958e305 + 1.14037728103254468762927980248285270e303 * I
exp(lambertw( DBL_MAX + DBL_MAX * I)) ≈ 2.557935739687930990678357670308497539e305 + 2.552239351260206850940540465216562109e305 * I
exp(lambertw(-DBL_MAX + DBL_MAX * I)) ≈ -2.546517666521172009117885938485236756e305 + 2.563606662249022010249963578079392704e305 * I
exp(lambertw(DBL_MAX * I)) ≈ 5.70197134852380166291426603783285580e302 + 2.55633545450941131201825034698564095e305 * I

For more informations

About Convergence check and complex input → www.hpmuseum.org/forum/thread-15004-post-137100.html

Reference

"Lambert W-function", Wolfram MathWorld
"Why W?", Hayes, B. (2005). American Scientist. 93 (2): 104‐108.
"Lambert W function", Wikipedia
"The Lambert W function poster", Ontario Research Centre for Computer Algebra.
"Puiseux series", Wikipedia
"Newton's Method", Wolfram MathWorld
"Householder's Method", Wolfram MathWorld
"Convergence of Numerical Iteration in Solution of Equations.", Urabe Minoru, J. Sci. Hiroshima Univ. Ser. A 19 (1956), no. 3, 479--489. doi:10.32917/hmj/1556071264.
"Improved Complex Division", Michael Baudin, Robert Smith, 2011
GSL - GNU Scientific Library
gnuplot demo - 3D plotting complex functions with color mapping using pm3d
"Mathematics Written in Sand", W. Kahan, University of California @ Berkeley, Nov. 1983

See Also